以下の3つの設問(問12-12,問12-19,問12-29)の回答から,回答者ごとの活動性尺度を算出できるものとします(「はい」2点,「どちらともいえない」1点,「いいえ」0点.たとえば3問すべてに「はい」と回答していると活動性尺度は6点.)
このとき,この活動性尺度の得点と,「人の暮らしかた」設問(問10)の回答の間にどのような関係があるのかを知りたいとします.
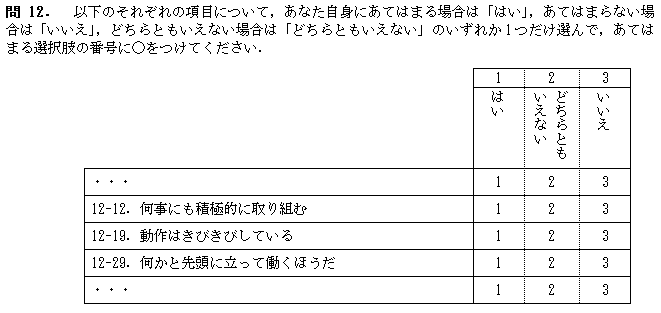

これをクロス集計してみると,以下のようになります.
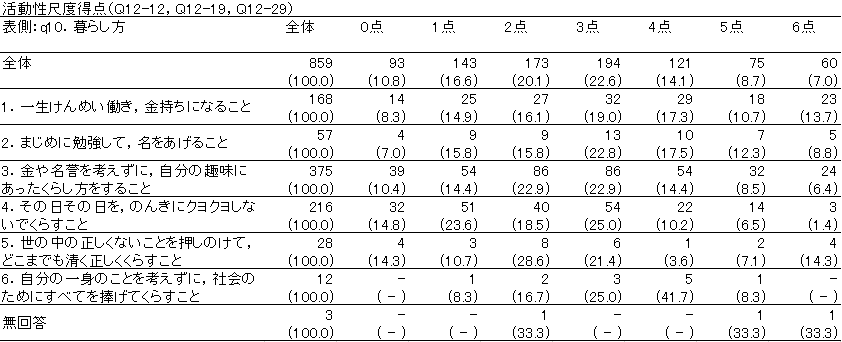
このクロス表に対して対応分析を行ってみた結果は以下の通り.
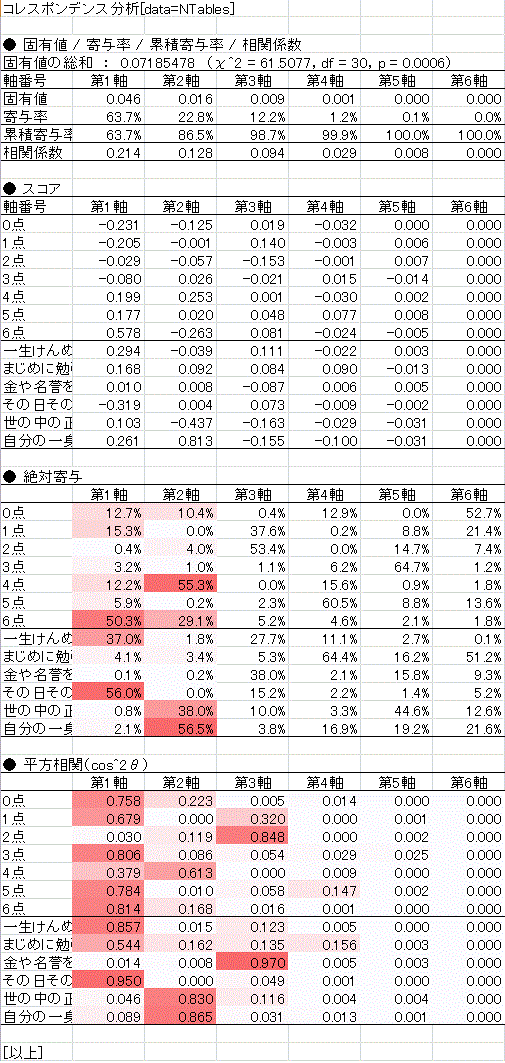
累積寄与率をみると,2軸まで見ればおおよその概況はわかりそうです(86.5%).平方相関を見ると尺度得点の「2点」,人の暮らし方の「金や名誉〜」についてはあまり1軸,2軸には関係なさそうです.こうしたことを踏まえて,1軸×2軸の散布図を描いてみます.
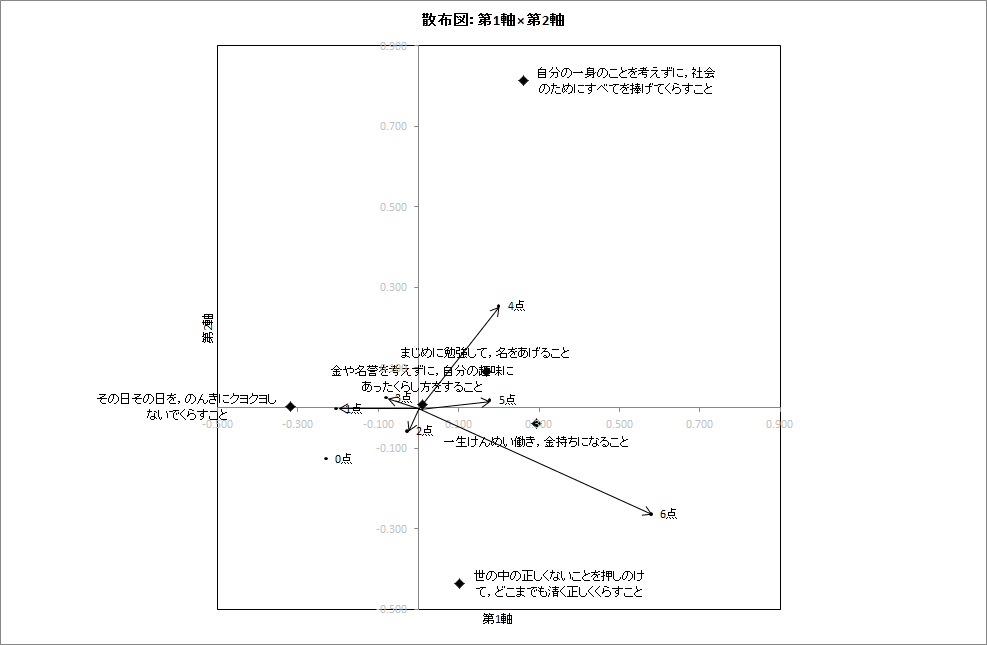
散布図を見ると,おおむね第3象限→第2象限→第1象限→第4象限の順に活動性尺度得点が大きくなっています.この方向で人の暮らし方設問の各選択肢を見ると,「その日その日を〜」→「自分の一身を」「まじめに勉強して〜」→「一生懸命はたらき〜」→「世の中の〜」といった順に選択肢が対応しているようです(角度に注目してください).
こうしてみると,確かに「のんきに暮らす」より「まじめに勉強して,名をあげる」,さらには「どこまでも清く正しくくらす」といったほうが,より「活動性」が高いであろうことは納得ができます.
こうした活動性尺度得点と暮らし方の対応関係は,対応分析を通じては容易に読み取れますが,もとのクロス表をただながめていても,なかなか見えてきません.
なお,こうしてみると,第3象限から右回りに尺度得点が大きくなっており,分析結果としては2次元分の情報を見ていますが,情報量としては一次元分の情報しかない可能性があります(馬蹄形問題).ここでは無理に各次元に意味を見出そうとしないほうが良いかもしれません.
- 計算(数式)については右記参照→https://www.facebook.com/553674608023080
- 「絶対寄与」「平方相関(相対寄与)」については右記も参照→http://www.facebook.com/293428184047725
- 平均値表に対する対応分析も可能→http://www.facebook.com/232019753521902
- 対応分析の実行例については右記も参照→http://t-news.jp/
- なお,対応分析において,行要素と列要素を同時布置することについての根拠は右記http://www.facebook.com/257206221003255